This page attempts to explain exactly how AuctionDB calculates the market value of items. AuctionDB uses an algorithm with a bunch of steps to make it as accurate as possible while using as little memory / disk space to store the data as possible.

Let's use the following data set as an example (assume these are gold values and each number represents the buyout of a single item):

{5, 13, 13, 15, 15, 15, 16, 17, 17, 19, 20, 20, 20, 20, 20, 20, 21, 21, 29, 45, 45, 46, 47, 100}

Performing a simple average of this data set would give you a market value of 25.79 which is obviously too high. AuctionDB calculates the market value in multiple steps which attempt to correct for outliers, give a moving value over time, and give a much more accurate market value in general than a simple average.

Step 1:

It is easy to see that the value of the item depends on how many is typically bought at a time. If you bought the 5 cheapest auctions in this example, you'd pay 12.2 gold per item. If you bought the 15 cheapest, you'd pay 16.3 gold per item. This is an inherent weakness with most market value estimates. AuctionDB attempts to factor this into its market value.

It is assumed that the number of an item that is required on average is proportional to the number currently on the auction house. This assumption turns out to be pretty accurate. For example, there is more hypnotic dust on the auction house than greater celestial essences as hypnotic dust is used in much greater quantities than greater celestial essences. The same can be said for cloth, leather, ore, volatiles, and other items where the quantities required by trade skills are larger.

AuctionDB uses this to detect more subtle outliers. After it is through 15% of the auctions, any increase of 20% or more in price from one auction to the next will trigger the algorithm to throw out that auction and any above it. It will consider at most the lowest 30% of the auctions. In the example data above, there are no large increases in price between 15 and 30 percent of the way through, but it would totally ignore everything after (but not including) the 16 because that's the last number in the bottom 30% of the data. It would not ignore the 13 even though it's more than 20% greater than 5 because it is not yet 15% of the way through the data.

After step 1, the data set looks like this:

{5, 13, 13, 15, 15, 15, 16}

Step 2:

We now simply take the average of the data that survived step 1. In this case, the average is 13.143. Now, we find the standard deviation for our data. Our data has a standard deviation of 3.761.

In this step, AuctionDB throws out any data points that are more than 1.5 times the standard deviation away from the average. In this example, it throws out any data points that are not between 7.502 and 18.785 which means the 5 will get thrown out.

After step 2, the data set looks like this:

{13, 13, 15, 15, 15, 16}

Step 3:

Finally, we calculate our current market value by simply taking the average of the remaining data points. In this example, our final market value is 14.5. This method ensures that no poisoning of our market value can take place by those who post high volume items at astronomical prices. It also gets rid of more subtle outliers to determine the average.

Step 4:

I bet you thought we were done...but no, we are just getting started! So far we have determined the current market value of an item based on one scan. But we want a moving market value that adjusts over time to get rid of market fluctuation. At this point, AuctionDB throws out all the individual auction data and for the purposes of market value, only cares about two pieces of data: the day on which this market value was determined and the current market value itself. Again, this "current market value" isn't what shows up as the final market value because we need to take into account previous scans' market values.

Essentially, we are going to take a weighted average of the previous 14 days' market values plus today's. First, let me explain how these "daily market values" are calculated. AuctionDB will store the market values from every scan you've done today, but once it becomes tomorrow (and you log in), it will combine the market values from all your scans into a single market value using a simple average. For the purposes of calculating the market value at this instant, we also average today's scans but each individual scan is still stored separately in the saved variables file until the next day. So, now we're left with a list of daily market values. Here is a graph of the weighting we are going to be using:

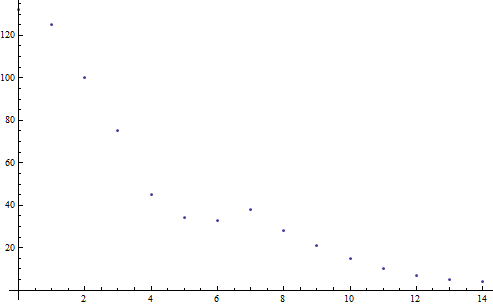
The x- axis is the number of days old the data is and the y-axis is the weight (on an arbitrary scale). As you can see, the recent data is very heavily weighted. This results in the data having a "half life" of a little over 2 days.